More poppycock: crop-factor equivalence

I discussed a few instances of poppycock in photographic literature here. On the present page, I discuss the concept of crop-factor equivalence, frequently used to compare the lenses used on different sensor sizes, and subsequently argue that there is no such thing as crop-factor equivalence.

Crop-factor equivalence

The first mass-produced DSLRs (as opposed to the first DSLRs in absolute terms, which were extremely expensive and extremely awkward cameras that only a professional photographer could possibly love, let alone afford) had APS-C sensors, roughly half the surface of a 36 x 24 mm film frame. The writers of promotional materials immediately got busy to try and make this format comprehensible to mere mortal photographers by comparing it with film SLRs. It was tacitly assumed, among other things, that all photographers potentially interested in purchasing an APS-C DSLR were already familiar with film SLRs and the 35 mm film in metal cartridges, and therefore this film format became overnight the golden standard for comparing the sizes of DSLR sensors. This is where the craze about crop-factor equivalence originated.

Simply stated, crop-factor equivalence has nothing to do with frame cropping or image cropping. A better term would probably be focal-length equivalence. This term tells you which focal lengths gives you the same angle of view (at infinity focus) on sensors of different sizes. A larger sensor always requires a longer lens focal length to give the same angle of view.

It is also very unfortunate that full-frame has come to indicate digital cameras with 36 x 24 mm sensors. All digital cameras, regardless of sensor size, fill their frames and sensors up to their edges with an image. A digital camera with a sensor half the area of a 35 mm film frame does not record only half the image viewed through the camera's viewfinder. Besides, a digital image has no physical size. The property of a digital image closest to size is its pixel count, which is largely independent of sensor size. You can get images with the same pixel count from full-frame, APS-C, Micro 4/3 cameras and even from the extremely small sensors of mobile phones. Different sensors can give you an extremely different pixel-count even when their physical size is the same. With sensor-shift technology, you can get images that contain several times more pixels than the photodiodes on the sensor that generated the image, so the number of photodiodes is not the upper limit of pixel count.

Crop-factor equivalence is a favorite discussion subject for people obsessed with comparing cameras of different sensor sizes. This category of people may be largely composed of persons who spend more time talking and writing about cameras and lenses than using them. Every photographer, through the use of his or her own cameras and lenses, acquires an instinctive understanding of approximately how wide a field of view each of these lenses produces on one's camera. The owner and user of an APS-C camera knows that a 21 mm lens is roughly at the borderline between a medium and an extreme wideangle, while a 35 mm is a "normal" lens and a 100 mm is a "medium-longish" telephoto. For the user of a full-frame camera, the corresponding focal lengths are roughly 28, 55 and 135 mm. For a Micro 4/3 user, they are 14, 28 and 70 mm.

Now that you understand crop-factor equivalence, I am going to show you that there is no such thing as equivalent lenses on different sensor formats.

Depth of field

It is often stated that the depth of field (DOF) of a lens mounted on a micro 4/3 cameras, at the same field of view and lens aperture, is substantially higher than a lens providing the same field of view, at the same aperture, on a full-frame camera. This is often used as an argument that full-frame cameras are inherently better than Micro 4/3 because the former provide a lower DOF, said to better isolate the subject from its background and foreground.

Although I firmly believe that a high DOF often is a good idea (as long as it does not entail an excessive loss of image resolution), I will not try to make my point with an extensive discussion. Instead, I will only make three examples:

• A higher DOF means that there is always a better chance that the important features of your subject will be in focus, even when AF does not lock onto the part of the subject that you regard as most important, or when a subject is moving too quickly or erratically for AF to reliably track it. 
• With good lenses, a higher DOF means that you often have the luxury of opening up the aperture by one or two stops, and shoot at a higher shutter speed without needing to increase the ISO. As a bonus, you also get less diffraction.
• A paper-thin DOF is not the way our eyes work. Besides providing a remarkably high DOF, our eyes automatically and instantly refocus on the part of the subject at the center of our field of view. Unless you need new glasses, are of advanced age, or are otherwise visually impaired, you will normally not perceive parts of your field of view as out of focus, because your attention is on the part that is always kept in focus. Classic paintings mimic our subjective perception rather than faithfully recording optical phenomena, and consequently, virtually always display an infinite DOF. Not because all parts of the scenery were actually in focus at the same time, but because the painter was only aware that, wherever he/she looked, that part appeared in focus to him/her.

In modern photography, a shallow DOF has been romanticized to such an extent that it is now often regarded as "more artistic" than a deep DOF. A shallow DOF was actually forced upon early photographers by the technical limitations of poor ambient illumination, low sensitivity of the photographic materials, and very large (by modern standards) camera formats. Present photographers may be enamored with low DOF simply because it reminds them of the early days of photography and movies, and because a low DOF is expensive to achieve with modern equipment.

Depth of field is given by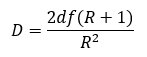

where D = depth of field, d = diameter of the circle of confusion, f = f-stop aperture, and R = reproduction ratio, or magnification. The above formula is a simplification that takes into account neither the pupil ratio of the lens nor diffraction (except as it relates to d), but is adequate for the present discussion. We will use it to compare the DOF provided by a 50 mm f/2 lens on full-frame and its crop-factor equivalent 25 mm f/2 on Micro 4/3. If you need a quick reminder of what magnification is and how to compute it, read here.

In order to make a comparison that actually makes sense, we assume that both cameras have 20 Mpixel sensors. On each image, we also assume that d is equal to the physical width of one pixel, so that both sensors are allowed to provide an image resolution at the Nyquist limit. This is the maximum theoretical (although often approached in practice) and best-case resolution of a sensor with discrete photodiodes. We also assume that the lenses we are using do not limit the image resolution. A typical 20 Mpixel Micro 4/3 sensor is 17.3 mm wide and provides 5184 pixels along this dimension, i.e, each pixel is 3.33 by 3.33 μm. Assuming that a full-frame sensor is twice as wide and twice as high as a Micro 4/3 (which is not exactly true, but close enough), full-frame pixels are 6.66 by 6.66 μm.

The above DOF formula breaks down at infinity focus, where R = 0. Instead of infinity, let's assume a relatively large distance between camera and subject, i.e. a low magnification. I will arbitrarily choose a magnification of 1/100 (i.e. 0.01) as an example. Applying the DOF formula to full frame gives (2 * 6.66 * 10^-6 * 2 * (0.01 + 1)) / 0.01², where * is multiplication. Note that the unit of length used in the calculation is m. We can further approximate the (0.01 + 1) term to 1. The result is a DOF of 0.27 m for the 50 mm f/2 on full frame.

When computing DOF of the 25 mm f/2 lens on Micro 4/3, we must first of all allow for the fact that, to yield the same field of view on Micro 4/3, R must be reduced by half, i.e. R = 0.005. Then, d must also be reduced to one-half, i.e. 3.33 μm. Thus, the calculation becomes (2 * 3.33 * 10^-6 * 2 * (0.005 + 1)) / 0.005², i.e. 0.53 m. The crop-factor equivalent lens on the smaller format has a significantly higher DOF (twice, in fact), when both lenses are used close to infinity focus.

If we repeat the calculation for the 50 mm f/2 on full-frame used at R = 1, we obtain a DOF of 53.3 μm. For the 25 mm f/2 on Micro 4/3, R = 0.5 gives the same field of view as R = 1 on full-frame, and the DOF becomes 107 μm. DOF of the Micro 4/3 crop-equivalent lens is still twice as much as the full-frame lens.

Therefore, crop-factor equivalent lenses are not equivalent, when it comes to DOF. At the same lens speed, a camera with a larger sensor will provide a lower DOF. Therefore, if you seek a lower DOF, it helps to choose a camera with a larger sensor, in addition to a fast lens. On the other hand, a higher DOF is usually an advantage in macrophotography, as well as several other technical applications. For these applications, you can get a higher DOF, at the same lens aperture, with a smaller-sensor camera.

Diffraction

When it comes to diffraction, a smaller-sensor camera is affected to a larger extent than a larger-sensor camera. For example, on Micro 4/3 one should not exceed f/8, or in some cases f/11, lest blurring by diffraction becomes noticeable. A full-frame camera displays a similar amount of diffraction at f/16 to f/22. Crop-factor equivalent lenses are therefore not equivalent also with respect to diffraction.

An actual equivalence 

From the above discussion, it seems that there is no crop-format equivalence between the two formats, at least in the simplistic way it is generally assumed. To observe an actual equivalence in multiple respects, one must lower the aperture by two stops for the Micro 4/3 format, when comparing the latter with full frame. A Micro 4/3 sensor at effective f/8 receives the same amount of light at the same exposure time, over its smaller sensor surface, as a full-frame sensor at effective f/16. If one compares DOF, the lens on Micro 4/3 generates the same DOF at f/8, compared to a lens on full-frame at f/16. Diffraction at f/8 on Micro 4/3 has the same visible blurring effect on the recorded image as at f/16 on full frame.

This equivalence, however, fails in other respects. For example, f/8 on Micro 4/3 does not require the same exposure time as f/16 on full-frame at the same ISO, but only one-quarter the exposure time. Alternatively, at the same aperture and exposure time, ISO on Micro 4/3 must be set to one-quarter the value than on full frame to achieve full equivalence. Incidentally, this lower ISO compensates for the unavoidably higher low-light noise of Micro 4/3 versus full-frame sensors, thus creating one more equivalence factor.

Magnification in macrophotography

As discussed here, magnification is the dimensionless ratio between the size of the subject image on the sensor and the size of the subject.

As mentioned above, a smaller-sensor camera needs to work at a lower magnification, in order to produce the same field of view of a larger-sensor camera. For example, to achieve the same field of view that a full-frame camera achieves at a magnification of 2x, a micro 4/3 camera and lens only need to work at 1x.

Crop-factor equivalent lenses are thus not equivalent with respect to the absolute magnification they need to work at, in order to produce the same field of view.

Focus distance in macrophotography

Focus distance is the distance between lens and sensor, at a given magnification. When the lens is focused at infinity on the subject side, magnification is zero and focus distance (D_f ) equals the lens focal length (F):

D_f = F

Indeed, this is the very definition of lens focal length.

Since magnification is not relative to sensor size but a dimensionless number, and there is no such thing as "format-relative magnification" (as discussed here), at a non-zero magnification the focus distance only depends on lens focal length (F) and magnification (R):

D_f = F + FR

Working distance in macrophotography

The working distance of a lens is the distance between the lens and the subject. For an ideal thin lens, the working distance (D_w ) is given by

D_w = F + (F / R)

where F is the lens focal length and R the magnification. Note the partial similarity with the formula for focus distance. The two distances are measured on opposite sides of the lens, and when one of them increases, the other reduces accordingly. Also note that the lens can no longer project a focused image if either distance decreases to a value lower than the focal length (except when more lenses are added to the system, and reduce the combined focal length of the system).

A macro lens that behaves like an ideal thin lens needs to be positioned at a focus distance equal to twice its focal length, in order to produce a 1x magnification. The working distance, at this magnification, is also equal to twice the focal length. Thus, a 50 mm macro lens has a working distance of 100 mm at 1x, while a 25 mm has a working distance of 50 mm at the same magnification.

If one considers the field of view of lenses in the macrophotography range, things are slightly more complicated. The working distance for the 100 mm lens on full frame at 1x is 200 mm, as seen above. However, to produce the same field of view, the 50 mm lens on Micro 4/3 needs to be focused at 0.5x, not 1x. At 0.5x, the working distance of the 50 mm lens is 50 + (50 / 0.5) = 150 mm. If you use a 100 mm lens on Micro 4/3, at 0.5x its working distance is 300 mm. In other words, a crop‑factor equivalent lens is not equivalent in working distance. At the same field of view of the 100 mm at 1x on full frame, a crop-factor equivalent lens on Micro 4/3 will give you a working distance shortened by 25%. On the other hand, using the same lens on both full-frame and Micro 4/3, on Micro 4/3 the lens will give you the same field of view at a working distance 50% higher.

In general, a high working distance is most often desirable in macrophotography. A narrower angle of view is also advantageous in macrophotography, allowing you to record smaller subjects. Thus, using the same macro lens on Micro 4/3, compared to full frame, gives you the dual advantages of a higher working distance at the same field of view as on full frame, and a narrower angle of view than on full frame. Naturally, the lens must be capable of providing a sufficiently high image resolution on Micro 4/3, which requires resolving, across the smaller sensor area, twice the line pairs per mm as on full frame.

Nominal and effective aperture

The nominal lens aperture (A_n ), in an ideal lens, is determined by the focal length of the lens (F) divided by its diameter (d) :

A_n = F / d

The aperture is thus expressed as a ratio of two linear measurements, and is therefore dimensionless. Lens speed is the fastest aperture of the lens, obtained when the diaphragm is fully open. The terms "speed", "fast" and "slow", as applied to the lens aperture, refer to the exposure time. A lens is fast when it collects more light, and therefore allows a shorter exposure time. Just as a reminder, a higher f/ratio value means a slower lens that collects less light.

In real lenses, one often calculates the lens speed based on the diameter of the front element. Real lenses can have a slower speed than indicated by the F / d ratio, depending on their optical design, but normally not a higher speed (except for some fast lenses designed to focus at very close distances from the subject).

Lens aperture (sometimes called f/ratio) is usually written as f/ followed by a numerical value, typically higher than 1.

As seen above, to increase magnification, one must increase the focus distance. The above formula to compute the aperture remains valid, but to compute the effective aperture (A_e), instead of F / d one must use the increased focus distance (F' ) :

A_e = F' / d

Thus, an increase in magnification is accompanied by a proportional increase in the effective aperture of the lens:

A_e = A_n (R + 1)

As seen above, when a full-frame camera needs to operate at an R magnification to fill the sensor with an image of the subject, a Micro 4/3 camera can do the same at the lower magnification of R / 2. This implies that, assuming the same lens nominal aperture and field of view, the effective aperture of the Micro 4/3 lens increases by one stop at 0.5x, while the effective aperture of the full-frame lens increases by two stops at 1x. In practice, in macrophotography the smaller sensor, in spite of being one-quarter the area of full frame, collects one-half the amount of light of the latter, which reduces the inherent light-collecting advantage of full frame to only one stop.

In conclusion, it is a fallacy to think that, in macrophotography on Micro 4/3 you can apply the concept of crop-factor equivalent focal length, use a macro lens of half the focal length as on full frame, and everything will stay the same. In fact, everything will change. In particular, using crop-factor equivalent focal length when choosing a macro lens for a smaller sensor format may lead you to grossly overestimate the lens working distance, and to buy the wrong lens.

Conclusions

Crop-factor equivalence is, on the face of it, a simple and convenient way to compare the lenses used on different sensor sizes. A more detailed analysis, however, shows that this equivalence only applies to the field of view of the lenses at infinity focus, but fails to account for several other factors that are significantly non-equivalent.